パーセプトロンとは、複数の信号を入力として受け取り一つの信号を出力する関数のようなものです。
図を使って表すと、こんな感じです。
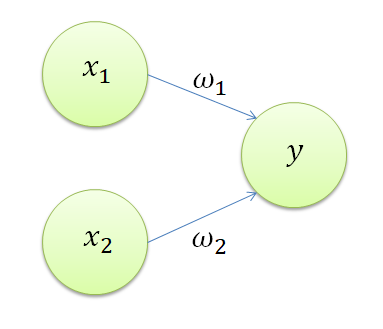
パーセプトロンにはANDゲート、ORゲート、NANDゲートがあります。
AND、OR、NANDの真理値表などの細かい説明は省略しますが、式を用いて記述すると以下のようになります。
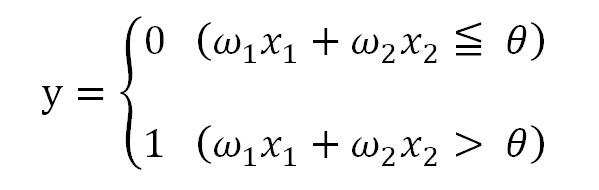
上の式で、(ω1,ω2,Θ)の値を変えることによって、ANDゲート、ORゲート、NANDゲートを実現できるのがパーセプトロンの特徴です。
例えば、(ω1,ω2,Θ)=(0.5,0.5,0.7)の例で考えてみましょう。
(x1,x2)=(0,0)・・・①
(x1,x2)=(1,0) ・・・②
(x1,x2)=(0,1) ・・・③
(x1,x2)=(1,1) ・・・④
を一つずつ代入してyの値を求めると、ANDゲートの働きをすることが分かると思います。
つまり、
①~③の時は、y=0 で
④の時だけ、y=1 となります。
面白くなってくるのは、「パーセプトロンの限界」の話です。
パーセプトロンの限界 XORゲート
パーセプトロンを使えば、AND、NAND、ORの3つの論理回路は実装することができました。
しかしながら、XOR(エクスクルーシブ OR)は1つのパーセプトロンで表現することができません。
つまり、下の式
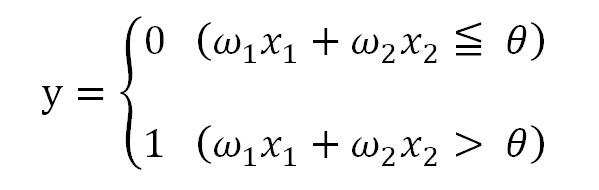
において、ωやΘの値をどのように変えても、XORゲートを満たすようなx1とx2の組み合わせが存在しないことを意味します。
なぜ、XORゲートはパーセプトロンで表すことができないのかを視覚的に考えてみることにします。
ANDゲートは線形
中学校で習った一次関数や高校で習った一次不等式の方が僕は考えやすくなるので、上の式のΘをbに置き換え、ω1=ω2=1、b=1.5として、x2について解きます。
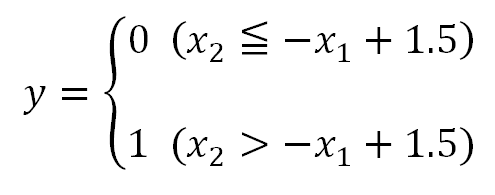
ここで、x1とx2を軸とする領域を考えてみることにします。
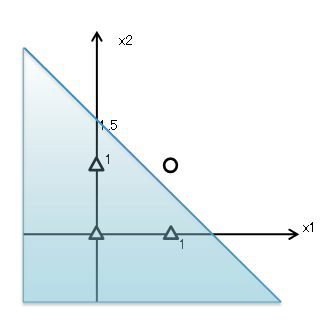
上のグラフで塗りつぶした領域は、

を満たす領域となりますので、この領域内ではy=0ということになります。
すなわち
(x1,x2)=(0,0)
(x1,x2)=(1,0)
(x1,x2)=(0,1)
において、
y=0
ということになります。
一方、塗りつぶしていない領域、すなわち
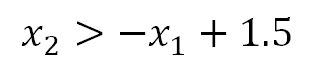
ではy=1ということになりますので、
(x1,x2)=(1,1)
において、
y=1
ということになります。
以上のことから、
![]()
という直線によって分けられた2つの領域がANDゲートの性質を満たすことが分かります。
ORゲートは線形
次にORゲートを確認してみることにします。
ω1=ω2=1、b=0.5として、x2について解きます。
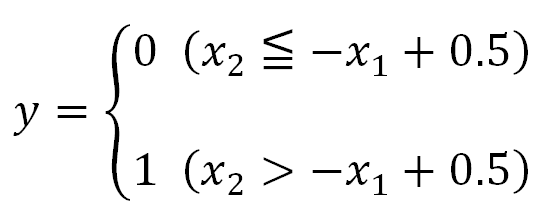
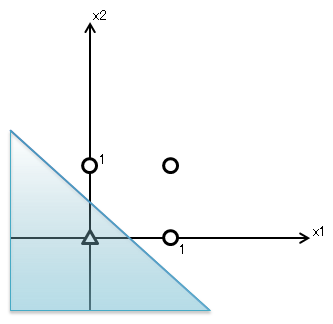
上のグラフで塗りつぶした領域は、
![]()
を満たす領域となりますので、
この領域内にある(x1,x2)は0ということになります。
別の言い方をすると、
(x1,x2)=(0,0)
において、
y=0
ということになります。
一方、塗りつぶしていない領域は
![]()
を満たす領域となりますので、
この領域内にある(x1,x2)は1ということになります。
別の言い方をすると、
(x1,x2)=(1,0)
(x1,x2)=(0,1)
(x1,x2)=(1,1)
において、
y=1
となります。
以上のことから、
![]()
という直線によって分けられた2つの領域がORゲートの性質を満たすことが分かります。





コメント