分類問題(※)で使われるソフトマックス関数は、次の式で表されます。
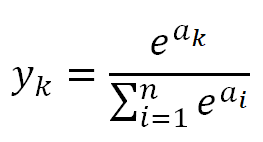
出力層:全部でn個
k番目の出力の分子:k番目の入力信号の指数関数
k番目の出力の分母:全ての入力信号の指数関数の和(kの値と無関係に総和を求める)
(※)例えば、写真に写っている人を読み込んで、その人の年齢が20歳未満、20代、30代、40代、50代以上のどこに分類されるか?というような問題を指します。
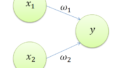
上のソフトマックス関数の式で、n=3の例を図で表すと下図で表現されます。
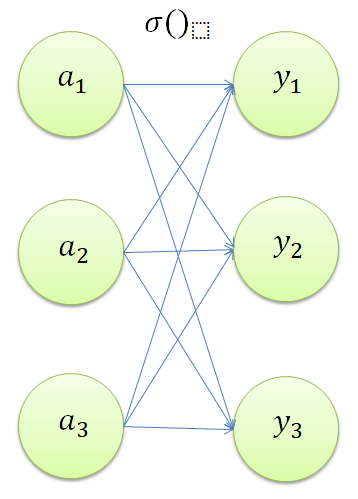
具体的な値をPythonを使って考えてみることにします。
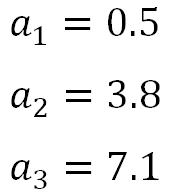
def SoftMax():
import numpy as np#入力信号の値
a = np.array([0.5,3.8,7.1])#ライブラリから指数関数を定義
exp_a=np.exp(a)#ライブラリから指数関数の総和を定義
print(exp_a)sum_exp_a=np.sum(exp_a)#総和を出力
print(sum_exp_a)SoftMax()
import numpy as np#入力信号の値
a = np.array([0.5,3.8,7.1])#ライブラリから指数関数を定義
exp_a=np.exp(a)#ライブラリから指数関数の総和を定義
print(exp_a)sum_exp_a=np.sum(exp_a)#総和を出力
print(sum_exp_a)SoftMax()
spiderで実行すると、以下の結果が得られます。
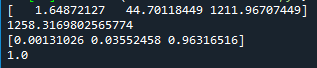
[ 1.64872127 44.70118449 1211.96707449] ・・・①
1258.3169802565774 ・・・②
1258.3169802565774 ・・・②
①は、配列内に設定した3つの入力値の指数関数をそれぞれ表しています。
つまり、
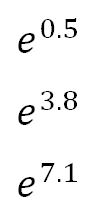
を計算したことになります。
②は①で求めた結果の総和となり、
=1258.31…
となります。
ソフトマックス関数では、この計算結果(1258.31…)が一つ一つの出力要素の分母となります。
最後に以下の記述を加えると、一つひとつの出力値が計算できます。
y=exp_a/sum_exp_a
print(y)
print(y)
ここまでのプログラムをspiderの画面で表示するとこんな感じとなります。
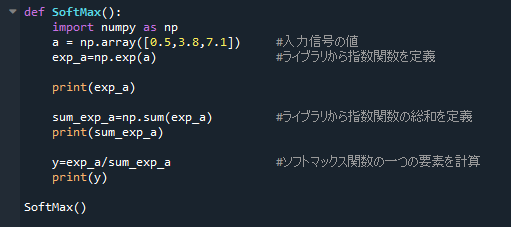
上のプログラムの出力結果です。

ソフトマックス関数の特徴
ソフトマックス関数の特徴は
ソフトマックス関数の出力値(要素)の総和=1
となることです。
先ほどのプログラムの最後に以下の命令を挿入して、実際に計算して確認してみます。
z=np.sum(y) #ソフトマックス関数の全ての要素の和
print(z)
print(z)
前節で求めた、y1~y3の要素を合計してzに代入し、zを表示する命令となります。
プログラム全体はこんな感じになります。

プログラムを実行すると、ソフトマックス関数で求めた出力値の総和が1となっていることが確認できます。
総和が1になるという性質を用いると、ソフトマックス関数の出力値を確率としてとらえることができます。
今回のケースでは、
y1=0.0013 なので、0.13%
y2=0.0352 なので、3.52%
y3=0.9631 なので、96.31%
となり、
問題に対して確率的な対応ができるようになります。
ソフトマックス関数の出力の総和が1となる理由
実際に分数の計算してみると、ソフトマックス関数の出力の総和が1になるのは当たり前だということが分かります。
n=3のケースで考えると、ソフトマックス関数の各出力は以下の通りとなります。
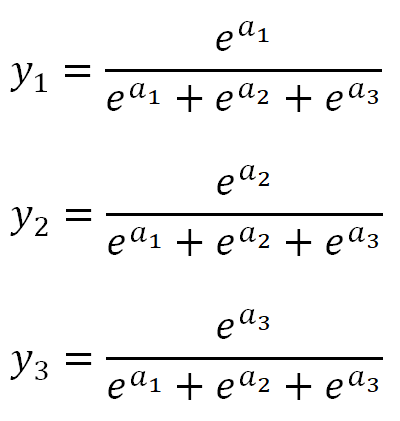
出力の総和をSとすると、
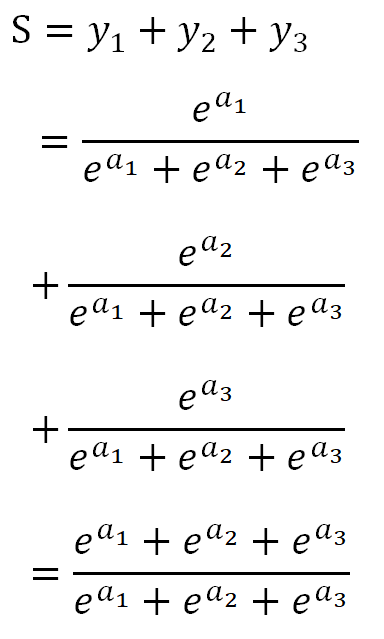
となり、分子=分母ですので、計算結果は1となります。
n=kと一般化しても、分子=分母となることは想像しやすいですね。





コメント